Time Complexity
- 1 minTime Complexity
Comparing Algorithms
Random access model (RAM)
- Simple operations take one time step
- Each memory access takes one step
- Loops and subroutines collections of simple operations
Can compute the number of time steps required for algorithm given a data config.
When dealing with data configurations:
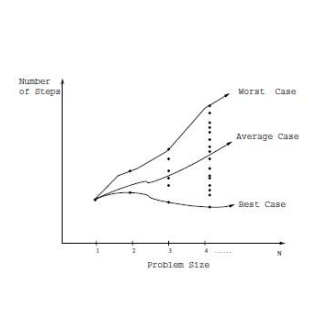
Analyze the algorithm in
- best case
- average case
- worst case→ most useful
Bubble sort analysis
| Operation | Best-case | Worst-case | Average-case |
|---|---|---|---|
| Comparisons | N(N-1)/2 | N(N-1)/2 | N(N-1)/2 |
| Swaps | N(N-1)/2 | N(N-1)/4 | |
| Total | N(N-1)/2 | N(N-1) | 3N(N-1)/4 |
But too much details here
Bubble sort optimized analysis
| Operation | Best-case | Worst-case | Average-case |
|---|---|---|---|
| Comparisons | N(N-1) | N(N-1)/2 | N(N-1)/2 |
| Swaps | 0 | N(N-1)/2 | N(N-1)/4 |
| Total | N-1 | N(N-1) | 3N(N-1)/4 |
Big Oh notation
- Simpler way of comparing algorithm performance
- Gross over lots of details
- Care about how the algorithm behaves for large problems $n \rightarrow \infty$
Definition
$f(n) = O(g(n))$ means there exists constant C such that $c.g(n) >= f(n)$ when $n \rightarrow \infty$ for large enough n when n > n0
Example:
$O(N(N-1)/2) = N^2$