Dynamic Programming
- 11 minsDynamic Programming
Notes
Is of two parts
- memoization
- tabulation
Fibonacci Memoization
Iterative Method
classic recursive implementation
int fib(int n){
if(n==1)return 1;
return fib(n-1)+fib(n-2);
}
But gets slower with increasing n. Visualize the problem as sub-problems which are nodes on a binary tree.
Complexity
O(2^n) → time
for fib(7)
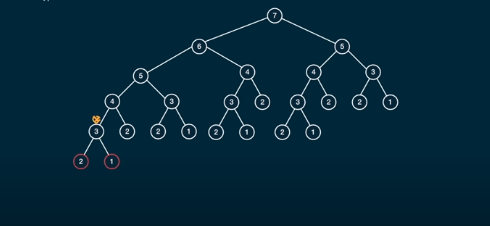
Same sub problems occur on each ends. Reuse calculation for similar sub trees.
Memoization method
Modified to store results in each iteration.
int fib(int n, std::map<int, int> &temp){
auto it = temp.find(n);
if(it!=temp.end()) return it->second;
if(n==1)return 1;
temp.insert({ n, fib(n-1,temp_map)+fib(n-2,temp_map)});
return temp.find(n)->second;
}
Grid Traveler
Starting form top-left corner how many ways to travel 2D grid to the bottom right of m*n.
function as
gridTraveler(m,n)
gridTraveler(2,3)->3
//base cases
gridTraveler(1,1)->1
gridTraveler(0,0)->0
gridTraveler(0,1)->0
gridTraveler(1,0)->0
Moving right and down in each iteration reveals sub problems until base cases are reached. Can be represented as binary tree where left is going down and right is going right. For a 2,3 grid can arrange as follows,
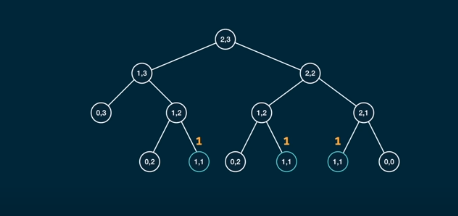After reaching base cases keep adding backwards to get the number of ways. The graph also reveals the different ways to reach required destination.
Iterative Method
int gridTraveler(m,n){
if(m==1&&n==1)return 1;
if(m==0||n==0)return 0;
return gridTraveler(m-1,n) + gridTraveler(m,n-1);
}
Complexity analysis
O(2^n+m) time
O(n+m) space
By looking through graph can be found out flipping the numbers still carries the same meaning. Hence
gridTraveler(a,b) = gridTraveler(b,a)
Memoization method
int gridTraveler(m,n, std::map<string, int> &temp){
string key = str(m) + ',' + str(n);
auto it = temp.find(key);
if(it!=temp.end()) return it->second;
if(m==1&&n==1)return 1;
if(m==0||n==0)return 0;
temp.insert({ key,gridTraveler(m-1,n,temp) + gridTraveler(m,n-1,temp);});
return temp.find(n)->second;
}
Complexity
O(m*n) time
O(m+n) space
Memoization Recipe (Can vary)
1. Make it work
- visualize problem as a tree
- implement the tree using recursion
- test it
2. Make it efficient
- add a memo object
- add a base case to return memo values
- store return values into the memo
canSum
Write function canSum(targetSum,numbers)
takes in targetSum and an array of numbers as arguments. The function should return a boolean indicating whether or not it is possible to generate the Sum using the array.
Assumptions
- element can be used as many times as you want
- all inputs nonnegative
canSum(7,[5,3,4,7])-> true
canSum(7,[2,4])->false
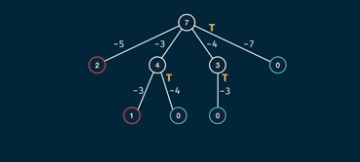
At least one branch is true at root return true. Hence one base case as true would solve the problem.
Iterative Method
bool canSum(int n, int* arr,int size){
if(n==0)return true;
if(n<0)return false;
for(int i=0;i<size;i++){
int r = n - arr[i];
if(canSum(r,arr,size))return true;
}
return false;
}
Problems
Counting Bits
Problem: https://leetcode.com/problems/counting-bits/
class Solution {
public:
vector<int> countBits(int n) {
vector<int> ans(n+1,0);
if(n==0)return ans;
ans[0]=0;
ans[1]=1;
for(int i=2;i<=n;i++){
ans[i] = ans[i/2] + i%2;
}
return ans;
}
};
Fibonacci Number
Problem : https://leetcode.com/problems/fibonacci-number/
int fib(int n){
if(n==0)return 0;
if(n==1)return 1;
int arr[n+1];
arr[0]=0;
arr[1]=1;
for(int i=2;i<=n;i++){
arr[i]=arr[i-1]+arr[i-2];
}
return arr[n];
}
Pascal’s Triangle
Problem: https://leetcode.com/problems/pascals-triangle/
class Solution {
public:
vector<vector<int>> generate(int n) {
vector<vector<int>> ans;
vector<int> tmp;
tmp.push_back(1);
ans.push_back(tmp);
for(int i=1;i<n;i++){
vector<int> temp = ans.back();
vector<int> curr;
curr.push_back(temp[0]);
for(int j=1;j<temp.size();j++){
curr.push_back(temp[j-1]+temp[j]);
}
curr.push_back(temp.back());
ans.push_back(curr);
}
return ans;
}
};
Divisor Game
Problem: https://leetcode.com/problems/divisor-game/
class Solution {
public:
bool divisorGame(int n) {
// # Theory:
// #
// # The game is winnable if and only if n is even.
// #
// # Proof by induction (informal):
// #
// # Consider the case n = 2. Alice then makes the only available move,
// # x = 1, leaving Bob to play the case n = 1. Bob now has no available
// # moves and so Alice wins.
// #
// # Now we need to show that, if Alice starts on an even number, she can
// # always guarantee that her next turn will also be on an even number.
// # From any n > 1, Alice can always play the move x = 1. Starting from
// # an even n, this leaves Bob with an odd n. An odd n has no even
// # factors by definition. Therefore, the only available choices of x for
// # Bob to play are now also odd. As a result, the next move for Alice
// # will always be even. Therefore, Alice can guarantee that she always
// # plays even numbers by forcing Bob to always play odd numbers.
// #
// # As Alice wins the game for the case n = 2, she also wins the game for
// # any even n. By the same logic, for any odd n, Bob can force Alice to
// # lose, by always leaving her to play with an odd n.
// return n%2==0;
bool arr[n+1];
if(n==1)return false;
if(n==2)return true;
arr[1]=false;
arr[2]=true;
for(int i=3;i<=n;i++){
arr[i]= !arr[i-1];
}
return arr[n];
}
};
Pascal’s Triangle II
Problem : https://leetcode.com/problems/pascals-triangle-ii/
class Solution {
public:
vector<int> getRow(int rowIndex) {
vector<vector<int>> ans;
vector<int> temp;
temp.push_back(1);
for(int i=1;i<=rowIndex;i++){
vector<int> curr;
curr.push_back(temp[0]);
for(int j=1;j<temp.size();j++){
curr.push_back(temp[j-1]+temp[j]);
}
curr.push_back(temp.back());
temp = curr;
}
return temp;
}
};
Min Cost Climbing Stairs
Problem: https://leetcode.com/problems/min-cost-climbing-stairs/
class Solution {
public:
int minCostClimbingStairs(vector<int>& cost) {
int n = cost.size();
vector<int> arr(n+1);
arr[0]=cost[0];
arr[1]=min(cost[1],cost[0]+cost[1]);
arr[n] = 0;
for(int i=2;i<n;i++){
arr[i]= min((arr[i-1]+cost[i]),arr[i-2]+cost[i]);
cout<<arr[i]<<" ";
}
arr[n] = min(arr[n-1],arr[n-2]);
return arr[n];
}
};